Trees and Graphs
Tree and Graph are common data structures in computer world, and actually Tree is a special type of Graph, Tree is a connected Graph without cycle.
Tree
Types of Trees
A tree is a data structure composed of nodes.
- Each tree has a root node.
- The root node has zero or more child nodes.
- Each child node has zero or more child nodes.
Trees vs. Binary Trees
Normally, tree has no child limit. If you use tree to represent English words including both cases, the node can have up to 52 children. Another example is phone number, its child node will have 10 nodes at most.
A binary tree is a tree in which each node has up to two children.
This is a binary tree from Wikipedia.
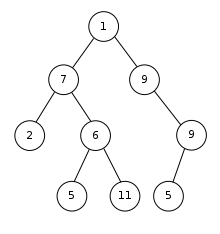
Binary Tree vs. Binary Search Tree
A binary search tree is a binary tree where each node satisfy a property:
all left nodes <= root < all right nodes.
This one is a binary search tree which all the left nodes are smaller than the right nodes of root.
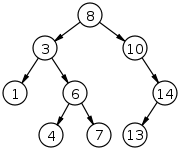
If we replace the node 7 with 12, it satisfy the property the lower level, but larger than the root which violate the property, then it will not a binary search tree.
Balanced vs. Unbalanced
A balanced tree is a tree that for each node, the height difference of left and right subtree is less than two.
This property can ensure that basic operations such as insert and search are running in O(logN).
Red-Black tree and AVL tree are two common balanced binary tree.
Complete Binary Tree
A complete binary tree is a tree in which every level is full filled, except the last level, and the last level will be filled from left to right. It means the last level has nodes range from 1 to 2^h, h is the height of the tree.
Full Binary Tree
A full binary tree is a tree in which every node has either 0 or 2 children.
Perfect Binary Tree
A perfect binary tree is a tree in which every node is fully filled except and last level full of leaves.
Binary Tree Traversal
- Pre Order visit root first, then left subtree and the right subtree last
void preorder(TreeNode root) {
if (root == null) return
println(root.val)
preorder(root.left)
preorder(root.right)
}
- In Order visit left subtree, then the root node and the right subtree last
void inorder(TreeNode root) {
if (root == null) return
inorder(root.left)
println(root.val)
inorder(root.right)
}
- Post Order visit left and right subtrees first, then the root node
void postorder(TreeNode root) {
if (root == null) return
postorder(root.left)
postorder(root.right)
println(root.val)
}
- Level Order visit the nodes level by level, from top to bottom
/** we use Queue to do the level order traversal
* need to be noted: how to know the level
**/
List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> results = new ArrayList<>()
if (root == null) return results
Queue<TreeNode> queue = new LinkedList<>()
queue.add(root)
while(!queue.isEmpty()) {
//here is the key
int sizeOfLevel = queue.size()
List<Integer> level = new ArrayList<>()
for(int i = 0; i < sizeOfLevel; i++) {
TreeNode node = queue.remove()
level.add(node.val);
if (node.left != null) queue.add(node.left)
if (node.right != null) queue.add(node.right)
}
results.add(level)
}
//done
return results
}
Binary Heaps(Min-Heaps and Max-Heaps)
A binary heap is a heap data structure that takes the form of a binary tree with two additional properties:
- it is a complete binary tree
- the root node is equal or bigger than child nodes, or less than child nodes. (the former is max-heap, the latter is min-heap).
It is used in heapsort originally.
Insert
- Insert into the most left open spot of the last level
- For Min-Heap, swap it with its parent if it’s smaller, repeat the step until reach the final spot
- For Max-Heap, swap it with its parent if it’s larger, repeat the step until reach the final spot
The runtime is O(logN).
Extract
- remove the top element, and replace it with the last node in the bottom level
- For Min-Heap, swap it with the smallest one of its child if it is larger, repeat the step until satisfy the property
- For Max-Heap, swap it with the largest one of its child if it is smaller, repeat the step until satisfy the property
The runtime is O(logN).
The above two operations are all related with the last spot in the bottom level of the tree.
Binary heap is commonly implemented with an array.
And the parent and children of any node can be found by arithmatic on array indices.
If the array’s index starts at 0,
- children at indices 2i + 1 and 2i + 2
- its parent at index floor((i - 1)/2)
If the tree root is at index 1,
- children at indices 2i and 2i + 1
- its parent at index floor(i/2) .
Trie Tree
A Trie is a variant of an n-ary tree (also called prefix tree) in which characters are stored at each node. Each path down the tree may represent a word.
It is commonly used in autocomplete dictionaries and web search engines.
An implementation example:
class Trie {
class TrieNode {
boolean isWord
TrieNode[] children = new TrieNode[SIZE]
}
//only handle lower-case English character
int SIZE = 26
TrieNode root
Trie() {
root = new Trie()
}
public void insert(String word) {
TrieNode cur = root
for(int i = 0; i < word.length(); i++) {
char ch = word.charAt(i)
if (cur.children[ch - 'a'] == null) {
cur.children[ch - 'a'] = new TrieNode()
}
cur = cur.children[ch - 'a']
}
cur.isWord = true
}
public boolean search(String word) {
TrieNode cur = root
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i)
if (cur.children[ch - 'a'] == null) {
return false
}
cur = cur.children[ch - 'a']
}
return cur.isWord
}
}
We can also use HashMap
Map<Character, TrieNode> children = new HashMap<>()
Graphs
A tree is one type of graph, it is an undirected graph in which any verticies are connected by exactly one edge, or a conntected acylic undirected graph. We have other types of graph, including Connected Graph, Complete Graph, Cycle Graph , Directed Graph and so on.
Representation
Graph has two common way to represent, one is adjacent list, the other is adjacent matrix.
Adjacent List
Verticies are stored as records or objects, and every vertex stores a list of adjacent verticies. There are additional data can be stored on the verticies.
Given edges, to create undirected graph using Adjacent List
List<List<Integer>> adjList = new ArrayList<>()
for (int i = 0; i < n; i++) {
adjList.add(new ArraList<>())
}
for(int[] edge: edges) {
adjList.get(edge[0]).add(edge[1])
adjList.get(edge[1]).add(edge[0])
}
Adjacent Matrix
It is a two-dimentional matrix, in which the rows represent source vertices and columns represent destination verticies. Only the cost of one edge can be stored between each pair of verticies.
The matrix could be a boolean one or integer one. For boolean one, true means two vertices connected, false means not connected. For integer matrix, 1 means connected while 0 means not connected.
martrix[i][j] means from source i to destination j.
Graph Search
The most common ways to search in a graph are depth first search (DFS) and breadth first search (BFS).
In DFS, we explore each branch completely before moving on to the next branch.
In BFS, we explore all the neighbors of one node before moving on to the next node.
Both DFS and BFS could be used to explore all the verticies of a graph, while BFS could be used to find the Shortest Path between two verticies.
DFS
Tree tarversals like preorder, inorder and postorder are all DFS, but one difference here is to mark visited node, or will face infinite loop.
void search(Node node) {
if (node == null) return
visit(node)
node.visited = true
for(Node child: node.adjacent) {
if (child.visited == false) {
search(child)
}
}
}
BFS
Tree’s level order traversal is also BFS. But like DFS, BFS also needs to consider to avoid visited node.
void search(Node node) {
Queue<Node> queue = new LinkedList<>()
node.visited = true
queue.add(node)
while(!queue.isEmpty()) {
Node n = queue.remove()
n.visited = true
for(Node child in n.adjacent) {
if (child.visited == false) {
child.visited = true
queue.add(child)
}
}
}
}
Disjoint Set (Union Find)
Given verticies and edges, how could we quickly determine whether two verticies are conntected? You may consider Shortest Path between these two vertices, but we have another option here, Disjoint Set.
Disjoint Set is also called Union Find, the primary use of it is to address connectivity between components of a network.
Terminologies
- Parent Node: the direct parent node of a vertex.
- Root Node: a node without a parent node.
Initially, all the nodes have themself as their parent. When we use union function to connect them, if two verticies are conntected, they will have a same parent node.
After the Find-Union operations, connected verticies are having same parent node while not conntected verticies’ parent nodes are different.
We could check their connectivity by checking whether their parent nodes are same or not.
Example code of Union Find.
public class UnionFind {
private int[] root
public UnionFind(int size) {
root = new int[size]
for(int i = 0; i < size; i++) {
root[i] = i
}
}
public int find(int x) {
while(x != root[x]) {
x = root[x]
}
return x
}
public void union(int x, int y) {
int rootX = find(x)
int rootY = find(y)
if (rootX != rootY) {
root[rootY] = rootX
}
}
public boolean isConnected(int x, int y) {
return find(x) == find(y)
}
}
Please expect that more content about Trees and Graphs later.
References
- https://en.wikipedia.org/wiki/Binary_tree
- Cracking the Coding Interview
- Trie
- https://en.wikipedia.org/wiki/Depth-first_search